Software Project Estimate Excel Template and Example

on
Free Software Project Estimate Template in Excel / Google Sheets  The template below has been successfully used in dozen of software development project. It calculates total project effort based on development estimates.  You can finetune the template to your project by adjusting corresponding percentages. Please follow the steps below to obtain full and realistic project estimate. Free Excel Software Project Estimate Template Free Google Sheets Software Project Estimate Template How to use this template Please follow the steps below to obtain full project estimate. Fill-in the cover.  It is important to list all the assumptions that make your estimate relevant. They may include the versions of frameworks, agreements with your client or contractors, disputable points in project scope definition, requirements etc. Place them onto Assumptions sheet. Create a WBS for your project. Noun-based WBS is preferable. List the work items in ESTIMATE sheet. Carefully read the contract, RFP or any
1

Mathematics of Successful Project Estimate

on

Task Effort as a Random Value

The effort need to complete a project task as well as the whole project effort can be treated as a random value. One of the goals of project estimate is to find a confidence interval for the project effort with high confidence level.

From empirical evidence we know that task probability distribution loos like this:

project task effort probability distribution

The long right tail is a sort of an implication of Parkinson's ("work expands so as to fill the time available for its completion.") and Murphy's laws ( "whatever can go wrong, will go wrong.").

Finding Expected Value

The first step is to find the expected value of the task estimate (strictly speaking we will estimate the expected value as the true distribution is unknown to us).

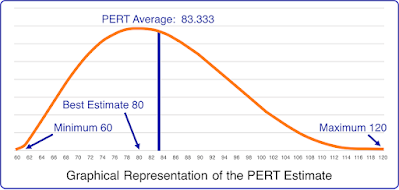
Three point estimation is probably the most famous technique to do that. However I will allow myself to criticize it a little. It is not always easy to get an adequate (minimal, maximum and realistic) estimate for a task. It also seems more intuitive and fast to make a realistic estimate and assess a risk, i.e. the confidence of the estimator in his estimate.

Shifting the realistic estimate to the right by adding a risk or using Three Point technique will give a good enough estimate of the task's expected value.

Adding things up

It is not obvious and needs proof that project estimate is equal to the sum of estimates of its tasks. One of the greatest math theorems, the Central Limit Theorem can help us here. It states that with some assumptions (independent random values, large enough number of them) the distribution of sum of such values will be close to normal. 
Central limit theorem

Source

Increasing the confidence interval

It means that if we take the sum of out tasks' estimate as project estimate, we will only hit 50% probability to fit into our estimate. Pure math. This is why adding a project buffer is crucial for project success. Three point estimate even provides a numerical way to find such an interval with required confidence level. In simpler case you can add up 5% to 15% depending on your intuition and perception of overall project risk.

NB: The math above only works if the actual scope of your project (i.e. the list and contents of tasks)is the same as you estimated. Project buffer does not save you from new scope. It is managed by assumptions or even larger increase of the buffer.

Comments

Post a Comment